Chapter 2: Worksheet 2 Jack K. Cohen Colorado School of Mines
Limits
Suggested Problems
Section 2.2: 2, 4, 10
- Often we want to do various operations on a fixed function. Here's how:
f[x_] := x^3 + 3x^2
f[2]
f[x] /. x -> 2
f[t]
f[cat]
Table[f[n], {n, 1, 5}]
Plot[f[x], {x, -2, 2}]
Hand in the output from these commands. Notice carefully that the square brackets, underbar and colon in the original function definition must be just the way they are shown on the first line. Computer languages are notorious for being fussy about notation. (Caveat: there are occasions when it is correct and even necessary to omit the colon, we'll discuss that issue later, put it in for now when defining a function in .) Note also the use of a ``rule'' in line 3. Rules give an alternate way of evaluating functions—here there is little point, but see problem 2e below where it is used to avoid duplicate code (always a good idea, because with duplicate code you can easily update in one place and forget to update in the other).
- (Example 4) Find

 by each of the following methods:
by each of the following methods:
- Make a Plot of the fraction near the point x = 0. This often ``works'' even when, as in this case, the function is not defined at the critical point. You may generate a complaint if Plot happens to try the exact value x = 0—nonetheless, the Plot will be fine.
- Make a Table near x = 0.
- Most algebraic limits of the 0/0 form can be simplified to a form where ``plugging in'' works. Here, the technique used in Example 12 can be used to advantage. In other cases, standard tools such as factoring can be used advantageously.
- The Binomial Theorem says
(1 + x)n = 1 + nx + .... It turns out that this Theorem also works for fractional powers. In particular, accept for now that
(1 + x)1/2 = 1 + (1/2)x + ... for values of x near zero. Apply this to the case at hand to write
 = 5
= 5
 5(1 + x/50) and thus evaluate the given limit. Ahem. The square root approximation given here is an enormously useful weapon.
5(1 + x/50) and thus evaluate the given limit. Ahem. The square root approximation given here is an enormously useful weapon.
- Program of the Week: The straight forward use of Table doesn't ``home in'' on the critical point. Here is code that is more tuned for this purpose:
f[x_] := (Sqrt[x + 25] - 5)/x
a = 0;
ntimes = 5;
N[ Table[{x, f[x]} /. x -> a + 1/10^k, {k, 1, ntimes}] ] //TableForm
Try this code out. As it stands, the code explores the right limit; modify it to explore the left limit and report the results of running your modified code.
- Write a short essay giving the good and bad points of each of the above methods. Try to envision the situation for functions other than the specific one treated here.
- (2.2.8) Evaluate

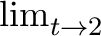 by method (c) and at least one other.
by method (c) and at least one other.
- (2.2.22) Evaluate

 by method (c) and at least one other.
by method (c) and at least one other.
- (2.2.32) Evaluate
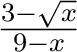
 by at least
two methods.
by at least
two methods.
- (2.2.35) Evaluate

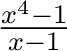

 -
- 
 by method (c) and at least one other.
by method (c) and at least one other.
- (2.2.36) Evaluate

 by two
methods.
by two
methods.

 by each of the following methods:
by each of the following methods:
 = 5
= 5
 5(1 + x/50) and thus evaluate the given limit. Ahem. The square root approximation given here is an enormously useful weapon.
5(1 + x/50) and thus evaluate the given limit. Ahem. The square root approximation given here is an enormously useful weapon.

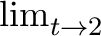 by method (c) and at least one other.
by method (c) and at least one other.

 by method (c) and at least one other.
by method (c) and at least one other.
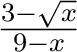
 by at least
two methods.
by at least
two methods.

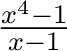

 -
- 
 by method (c) and at least one other.
by method (c) and at least one other.

 by two
methods.
by two
methods.